Generalized Integral Images

Konstantinos Derpanis, Erich Leung and Mikhail Sizintsev

Contact email: kosta at cse dot yorku dot ca


DoB flower garden example DoB cat example
Examples: Blob detection using our Difference of B-spline (DoB) detector, computed efficiently using the generalized integral image.


Overview:

    The integral image representation (known in graphics as summed area tables) popularized by Viola and Jones in the computer vision literature represents an efficient/fast manner for computing space variant box filter related features.  Briefly, the integral image representation is computed by a running sum image (i.e., the integral image) and the features are computed by linear weighted samples of the integral image.  More generally, by preintegrating the image n times and taking appropriate linear weighted samples one can generate the family of B-spline filters (see figure below), where the first order integral image realizes the zero order B-spline (box) filter.  We call this family of representations, the generalized integral image.
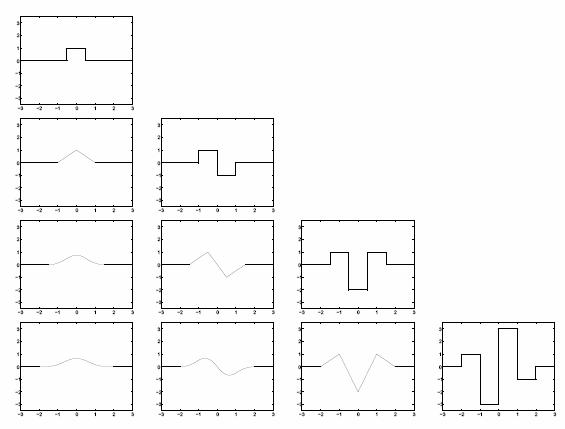B-splines
B-spline filters from orders zero to three (top to bottom) and their respective derivaties from zero to three (left to right)

    The generalized integral image formulation allows for the efficient formulation of a multitude of multi-scale feature representations, such as, interest point detectors (example figure shown at top) and smoothed differential filters.  The main advantages of making the integral order of the representation salient are two-fold: (1)  it allows for reducing the introduction of spurious distracting structures common to box filter-based approaches (filter smoothness increases as the B-spline order is increased) and (2) it allows for the reduction in the degree of anisotropicity in the filters which in turn results in the improvement in the rotation invariance of filter responses.  Importantly, these advantages are realized while still retaining the efficiency aspect of the original integral image formulation.  Ultimately, the selection of the integral image order is application dependent; a trade-off between speed in feature computation and accuracy in feature representation must be made.


Related Papers:
Derpanis, K.G., Leung, E.T.H. and Sizintsev, M., Fast Scale-space Feature Representations by Generalized Integral Images, International Conference on Image Processing, 2007. (short version)

Derpanis, K.G., Leung, E.T.H. and Sizintsev, M.,  Fast Scale-space Feature Representations by Generalized Integral Images, York University, Technical Report CSE-2007-01, 2007. (long version)

 Derpanis, K.G., Integral Image-based Representations, York University, memo, 2007.

Software:

Generalized integral image C++ code


Last updated: Seotember 30, 2007.