Reading material

Additional material

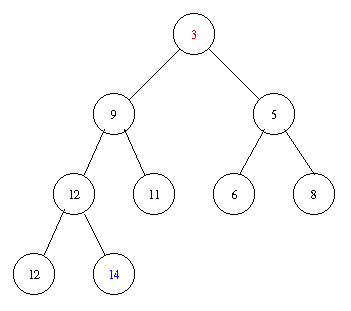
Removing the minimal element takes the following steps.

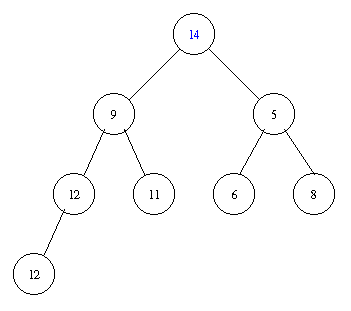
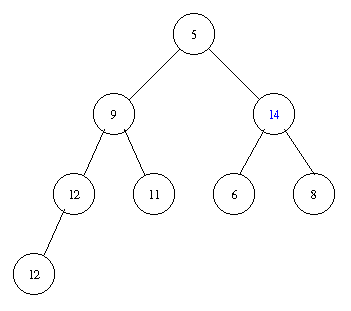
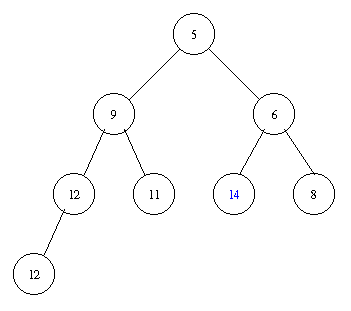
Inserting an element with key 8 takes the following steps.

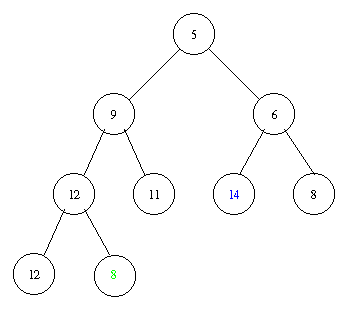
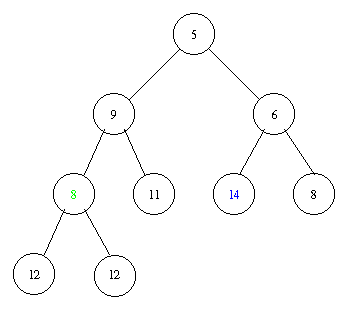
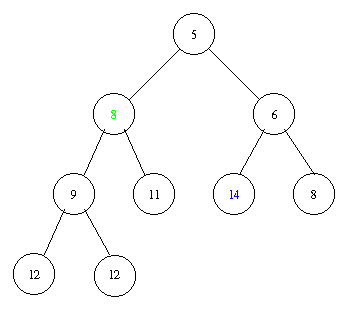
Implementation of a priority queue with a heap in pseudocode: PostScript and PDF

HeapPriorityQueue
PriorityQueueFullException
InPlaceHeapSorter

Question

/**
   Returns the minimum of the specified matrix.
   The specified matrix is assumed to have the same number of rows as columns.
  
   @param matrix a two-dimensional array of integers.
   @return the minimum of the specified matrix.
*/
public static Integer minimum(Integer[][] matrix)
{
    final int DIMENSION = matrix.length;
    PriorityQueue minQueue = new ?PriorityQueue(new IntegerComparator());
    for (int r = 0; r < DIMENSION; r++)
    {
        PriorityQueue rowQueue = new ?PriorityQueue(new IntegerComparator());
        for (int c = 0; c < DIMENSION; c++)
        {
            rowQueue.insertItem(new Item(matrix[r][c], matrix[r][c]));
        }
        Object element = rowQueue.removeMin();
        minQueue.insertItem(new Item(element, element));
    }
    return minQueue.removeMin();
}